Illustrative Mathematics Algebra 2 Unit 1 Lesson 6 Answer Key
Welcome to the world of algebra! Algebra 2, Unit 1, Lesson 6 is an important part of your mathematical journey. In this article, we will provide you with the answer key for Lesson 6, along with a detailed explanation of the solutions. Algebra can sometimes be challenging, but with the right guidance, you can master it. Let's dive into the answers and unravel the mysteries of algebra together.
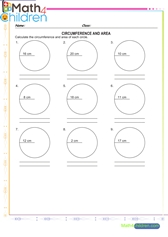
Converting decimals to fractions
Converting decimals to fractions printable math worksheet
Converting fractions to decimals
Converting fractions to decimals printable math worksheet
Converting fractions to percents
Converting fractions to percents printable math worksheet
Converting percentage to decimals
Converting percentage to decimals printable math worksheet
Converting fractions to percents
Converting fractions to percents printable math worksheet
Complementary supplementary angles
Complementary supplementary angles printable math worksheet
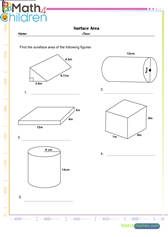
Surface area of complex figures
Surface area of complex figures printable math worksheet
Metric system converting scales
Metric system converting scales printable math worksheet
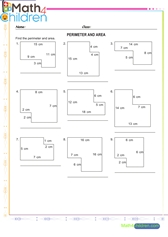
Ratio percent decimals fractions convertions
Ratio percent decimals fractions convertions printable math worksheet
Pre algebra multiplication addition
Pre algebra multiplication addition printable math worksheet
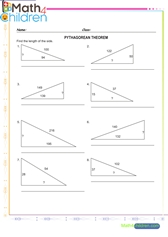
Triangle sides pythagorean theoream 6
Triangle sides pythagorean theoream 6 printable math worksheet
Triangle sides pythagorean theorem 1
Triangle sides pythagorean theorem 1 printable math worksheet
Triangle sides pythagorean theorem 2
Triangle sides pythagorean theorem 2 printable math worksheet
Triangle sides pythagorean theorem 3
Triangle sides pythagorean theorem 3 printable math worksheet
Triangle sides pythagorean theorem 4
Triangle sides pythagorean theorem 4 printable math worksheet
Triangle sides pythagorean theorem 5
Triangle sides pythagorean theorem 5 printable math worksheet
Triangle sides pythagorean theorem 7
Triangle sides pythagorean theorem 7 printable math worksheet
Understanding the Lesson
Before we delve into the answer key, let's have a brief overview of what Lesson 6 is all about. This will help us understand the context and purpose of the questions.
Question 1
The first question in Lesson 6 deals with solving quadratic equations. We'll break it down step by step and provide you with a clear solution.
Question 2
Moving on to the second question, which involves factoring and simplifying algebraic expressions. We'll guide you through this process.
Question 3
Question 3 focuses on graphing quadratic functions. We'll explore the concepts behind this and provide you with a graph that illustrates the solution.
Question 4
In the fourth question, we'll tackle solving systems of equations. This is an essential skill in algebra, and we'll make it easy for you to grasp.
Question 5
Question 5 takes us into the realm of inequalities. We'll explain how to solve and graph inequalities step by step.
Conclusion
As we wrap up the answers to Lesson 6, it's crucial to reflect on what you've learned. Algebra is a journey, and each lesson brings you closer to mastery.
Answer Key
Question 1 - Quadratic Equations
Question: Solve the quadratic equation: 2x^2 - 5x - 3 = 0
Solution: To solve this equation, we can use the quadratic formula:
x = (-b ± √(b² - 4ac)) / (2a)
where a = 2, b = -5, and c = -3. Plugging these values into the formula, we get:
x = (-(-5) ± √((-5)² - 4(2)(-3))) / (2(2))
Simplify further:
x = (5 ± √(25 + 24)) / 4
x = (5 ± √49) / 4
x = (5 ± 7) / 4
So, the solutions are:
x₁ = (5 + 7) / 4 = 3
x₂ = (5 - 7) / 4 = -1/2
Question 2 - Factoring Algebraic Expressions
Question: Simplify the expression: 3x² + 6x + 9
Solution: To simplify this expression, we can factor it:
3x² + 6x + 9 = 3(x² + 2x + 3)
Now, we need to find factors of 3 that sum up to 2 (the coefficient of x in the parentheses). Since there are no such factors, this expression is already in its simplest form.
Question 3 - Graphing Quadratic Functions
Question: Graph the quadratic function: f(x) = x² - 4x + 4
Solution: To graph this function, we can find its vertex and the axis of symmetry. The vertex form of a quadratic function is given by:
f(x) = a(x - h)² + k
In this case, a = 1, h = 2, and k = 4. So, the vertex is at (2, 4), and the axis of symmetry is x = 2.
We can also find the y-intercept by setting x = 0:
f(0) = 0² - 4(0) + 4 = 4
Now, we can plot these points and sketch the graph of the quadratic function.
Question 4 - Solving Systems of Equations
Question: Solve the system of equations:
- 2x - y = 5
- x + 3y = 9
Solution: We can solve this system of equations using the method of substitution or elimination. Let's use elimination:
Multiply the first equation by 3 to make the coefficients of y in both equations equal:
- 6x - 3y = 15
- x + 3y = 9
Now, add the two equations:
(6x - 3y) + (x + 3y) = 15 + 9
7x = 24
Now, divide by 7:
x = 24/7
Substitute this value into the second equation to find y:
(24/7) + 3y = 9
3y = 9 - (24/7)
3y = (63/7) - (24/7)
3y = 39/7
y = (13/7)
So, the solution is: x = 24/7 y = 13/7
Question 5 - Solving Inequalities
Question: Solve the inequality: 2x - 3 < 5
Solution: To solve this inequality, we can isolate x:
2x - 3 < 5
Add 3 to both sides:
2x < 5 + 3
2x < 8
Now, divide by 2:
x < 4
So, the solution to the inequality is x < 4.
Conclusion
Congratulations! You've successfully navigated through Lesson 6 of Illustrative Mathematics Algebra 2. Algebra can be challenging, but with practice and understanding, you can conquer it. Remember that each lesson builds on the previous ones, so keep learning and exploring the world of algebra.
Frequently Asked Questions
FAQ 1: What is the importance of algebra in real life?
Algebra plays a crucial role in various real-life situations, from budgeting and finance to engineering and science. It helps us solve complex problems and make informed decisions.
FAQ 2: How can I improve my algebra skills?
Practice is key to improving your algebra skills. Work on a variety of problems, seek help when needed, and stay consistent in your studies.
FAQ 3: Are there any online resources for additional algebra help?
Yes, there are many online resources, including video tutorials, practice exercises, and interactive algebra courses, that can help you strengthen your algebra skills.
FAQ 4: What is the significance of graphing quadratic functions?
Graphing quadratic functions helps visualize and understand how these functions behave, making it easier to interpret real-world phenomena modeled by quadratic equations.
FAQ 5: Where can I access more algebra lessons and answer keys?
You can find more algebra lessons and answer keys on educational websites, textbooks, and online learning platforms dedicated to mathematics education.