Algebra Identities | Algebra Identities Class 9
Hello math enthusiasts! Have you ever wondered about the magical world of Algebra and its intriguing identities? You're in the right place. In this article, we'll dive into the core of Algebra and discuss the key concept of Algebra Identities.
Converting decimals to fractions
Converting decimals to fractions printable math worksheet
Converting fractions to decimals
Converting fractions to decimals printable math worksheet
Converting fractions to percents
Converting fractions to percents printable math worksheet
Converting percentage to decimals
Converting percentage to decimals printable math worksheet
Converting fractions to percents
Converting fractions to percents printable math worksheet
Complementary supplementary angles
Complementary supplementary angles printable math worksheet
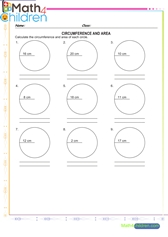
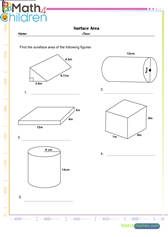
Surface area of complex figures
Surface area of complex figures printable math worksheet
Metric system converting scales
Metric system converting scales printable math worksheet
Ratio percent decimals fractions convertions
Ratio percent decimals fractions convertions printable math worksheet
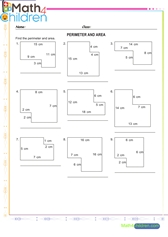
Pre algebra multiplication addition
Pre algebra multiplication addition printable math worksheet
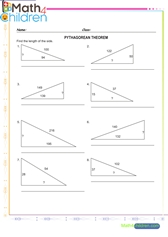
Triangle sides pythagorean theoream 6
Triangle sides pythagorean theoream 6 printable math worksheet
Triangle sides pythagorean theorem 1
Triangle sides pythagorean theorem 1 printable math worksheet
Triangle sides pythagorean theorem 2
Triangle sides pythagorean theorem 2 printable math worksheet
Triangle sides pythagorean theorem 3
Triangle sides pythagorean theorem 3 printable math worksheet
Triangle sides pythagorean theorem 4
Triangle sides pythagorean theorem 4 printable math worksheet
Triangle sides pythagorean theorem 5
Triangle sides pythagorean theorem 5 printable math worksheet
Triangle sides pythagorean theorem 7
Triangle sides pythagorean theorem 7 printable math worksheet
Understanding Algebra
Definition
Algebra, in its simplest form, is one of the broad areas of mathematics, alongside number theory, geometry, and analysis. It's the study of symbols and the rules for manipulating these symbols.
Importance of Algebra
Why should we bother with algebra, you ask? Well, it's fundamental in fields such as science, engineering, medicine, economics, and beyond. It allows us to formulate real-world problems and find solutions in a simplified manner.
What are Identities in Algebra?
Definition
Algebra Identities are equations that hold true for all possible values of their variables. They are the backbone of algebra and hold the essence of mathematical beauty and consistency.
Purpose of Algebra Identities
The main purpose of these identities is to simplify complex expressions and solve equations. They're like secret keys to unlocking the mysteries of algebraic equations!
Types of Algebra Identities
Algebra identities generally fall into three categories: Binomial identities, Factorization identities, and Trigonometric identities. Let's unravel each one step-by-step.
Binomial Identities
Binomial identities represent the expanded form of the power of a binomial. They help simplify calculations and solve problems faster.
Factorization Identities
Factorization identities are used to factorize certain algebraic expressions. These identities play a crucial role in simplifying complicated expressions and equations.
Trigonometric Identities
Trigonometric identities, while technically part of algebra, intersect with trigonometry. They relate the angles and lengths of triangles, proving incredibly useful in countless fields such as physics and engineering.
Understanding Binomial Identities
Definition
Binomial identities refer to the identities that involve the sum or difference between two terms. They are indispensable in dealing with polynomials and simplifying complex equations.
Examples and Applications
The most common example is the identity for the square of a binomial: (a+b)^2 = a^2 + 2ab + b^2. This identity makes it easier to square a binomial without performing the entire multiplication.
Understanding Factorization Identities
Definition
Factorization identities are essential tools for simplifying and solving algebraic expressions. They transform complex expressions into a product of simpler ones.
Examples and Applications
A typical example is a^2 - b^2 = (a+b)(a-b). This identity allows us to factor a difference of squares into the product of a sum and a difference, easing the solving process.
Understanding Trigonometric Identities
Definition
Trigonometric identities are equations involving trigonometric functions that hold true for all values of the occurring variables. They are the cornerstones of trigonometry and calculus.
Examples and Applications
One popular identity is the Pythagorean identity: sin^2(x) + cos^2(x) = 1. This crucial identity forms the basis of many mathematical proofs and solutions in trigonometry.
Why Learning Algebra Identities Is Essential
Algebra identities are not just abstract mathematical concepts. They help us simplify complex mathematical problems, making the problem-solving process more efficient. Plus, they lay the groundwork for advanced mathematical study.
Practical Applications of Algebra Identities
From computer science to architecture, algebra identities are employed in a multitude of areas. Whether you're calculating the trajectory of a rocket or designing a spiral staircase, you'll likely use an algebra identity or two.
Tips to Master Algebra Identities
Mastering algebra identities requires practice and patience. Work on as many problems as you can, and try to understand the underlying concepts rather than just memorizing the identities.
Conclusion
There you have it! We've taken a deep dive into the world of Algebra Identities, exploring their definitions, types, applications, and more. They are the unsung heroes of algebra, making our mathematical journeys smoother and more manageable. So, the next time you tackle an algebra problem, remember these invaluable tools at your disposal.
Frequently Asked Questions
-
What is the importance of Algebra Identities? Algebra identities are vital because they simplify complex mathematical expressions, making problem-solving more efficient.
-
What are the types of Algebra Identities? The three main types of algebra identities are Binomial Identities, Factorization Identities, and Trigonometric Identities.
-
How can I master Algebra Identities? The best way to master algebra identities is through consistent practice and understanding the underlying concepts.
-
Where are Algebra Identities used? Algebra identities are used in various fields including science, engineering, architecture, computer science, and more.
-
What is an example of a Binomial Identity? An example of a binomial identity is (a+b)^2 = a^2 + 2ab + b^2.
Algebra Identities Class 9: Simplifying Expressions and Solving Equations
-
Algebra is a fundamental branch of mathematics that deals with variables, symbols, and equations. In Class 9 mathematics, one of the key aspects of algebra is understanding and applying algebraic identities. These identities provide a set of rules and formulas that allow us to simplify expressions, solve equations, and manipulate algebraic terms efficiently. In this article, we will explore various algebra identities, their applications, and how they can be used to simplify expressions and solve equations.
Introduction
Algebraic identities are mathematical equations that hold true for any values of the variables involved. They provide a framework for performing operations on algebraic expressions, making calculations more manageable and efficient. In Class 9, students learn basic algebraic identities and use them to solve problems in algebra.
Basic Algebraic Identities
Basic algebraic identities are the foundation of algebraic operations. These identities help simplify expressions and make calculations more straightforward. Let's look at a few examples of basic algebraic identities:
- Identity: �+0=�
- Zero Property: �⋅0=0
- Commutative Property of Addition: �+�=�+�
- Commutative Property of Multiplication: �⋅�=�⋅�
- Associative Property of Addition: (�+�)+�=�+(�+�)
- Associative Property of Multiplication: (�⋅�)⋅�=�⋅(�⋅�)
These basic algebraic identities serve as building blocks for more complex algebraic manipulations.
Expanding Algebraic Expressions
Expanding algebraic expressions involves multiplying out brackets and simplifying the resulting expression. This process helps us understand the components of an expression and is useful for solving equations. Here's a step-by-step approach to expanding algebraic expressions:
- Distributive Property: �⋅(�+�)=�⋅�+�⋅�
- Expanding Double Brackets: (�+�)(�+�)=�⋅�+�⋅�+�⋅�+�⋅�
Let's illustrate the concept of expanding algebraic expressions with an example:
Example 1: Expanding an Algebraic Expression
Consider the expression: 2(�+3)
We can expand this expression using the distributive property:
2⋅�+2⋅3
This simplifies to:
2�+6
Expanding algebraic expressions allows us to work with individual terms and simplify complex equations.
Simplifying Algebraic Expressions
Simplifying algebraic expressions involves combining like terms and reducing the expression to its simplest form. This process helps in solving equations and making calculations more manageable. Let's explore some techniques for simplifying algebraic expressions:
-
Combining Like Terms: Terms that have the same variables and exponents can be combined. For example, 2�+3�=5� and 4�−2�=2�.
-
Applying the Distributive Property: The distributive property can be used to simplify expressions. For example, 2(�+3) can be simplified as 2�+6.
-
Removing Parentheses: Parentheses can be removed by multiplying out the terms. For example, (�+�)(�+�) can be expanded as �⋅�+�⋅�+�⋅�+�⋅�.
Let's work through an example to illustrate the simplification of an algebraic expression:
Example 2: Simplifying an Algebraic Expression
Consider the expression: 3�+2(�−4)−5
We can simplify this expression step-by-step:
3�+2�−8−5
Combining like terms:
5�−13
Simplifying algebraic expressions allows us to represent complex equations in a more concise and understandable form.
Factorizing Algebraic Expressions
Factorizing algebraic expressions involves breaking down an expression into its constituent factors. This process helps in solving equations and understanding the structure of an expression. Let's explore some techniques for factorizing algebraic expressions:
-
Common Factor: Identify if there is a common factor that can be factored out. For example, in 3�+6, we can factor out 3 to get 3(�+2).
-
Difference of Squares: If the expression consists of a difference of squares, it can be factored using the formula (�2−�2)=(�+�)(�−�). For example, �2−4 can be factorized as (�+2)(�−2).
-
Grouping: In some cases, grouping terms with common factors can help factorize an expression. For example, ��+��+��+�� can be factorized as �(�+�)+�(�+�), and then further simplified as (�+�)(�+�).
Let's factorize an algebraic expression to see these techniques in action:
Example 3: Factorizing an Algebraic Expression
Consider the expression: �2−4�−21
We can factorize this expression using the difference of squares:
�2−4�−21=(�−7)(�+3)
Factorizing algebraic expressions allows us to break down complex equations into simpler components, facilitating further calculations and problem-solving.
Solving Equations using Algebraic Identities
Algebraic identities play a crucial role in solving equations. They provide us with tools to manipulate equations and isolate variables. Let's explore the steps involved in solving equations using algebraic identities:
- Simplify the equation using algebraic identities and properties.
- Move all terms involving the variable to one side of the equation and the constants to the other side.
- Apply the appropriate algebraic identity or operation to isolate the variable.
- Solve for the variable by performing the necessary operations.
- Check the solution by substituting it back into the original equation.
Let's solve an equation using algebraic identities to demonstrate the process:
Example 4: Solving an Equation
Solve the equation: 2�−5=3�+2
Step 1: Simplify the equation by combining like terms:
2�−5−3�=2
Step 2: Move variables to one side and constants to the other:
2�−3�=2+5
Step 3: Apply the algebraic identity to isolate the variable:
−�=7
Step 4: Solve for the variable:
�=−7
Step 5: Check the solution:
Substituting �=−7 back into the original equation:
2(−7)−5=3(−7)+2
−14−5=−21+2
−19=−19
The solution �=−7 satisfies the equation.
By utilizing algebraic identities, we can solve equations and find values for variables, providing a powerful tool for mathematical problem-solving.
Applications of Algebra Identities
Algebra identities have numerous applications in various fields, including science, engineering, finance, and computer science. Here are a few examples:
-
Physics: Algebraic identities are used to derive equations in physics, such as the equations of motion and laws of thermodynamics.
-
Engineering: Algebraic identities are applied in solving engineering problems, such as electrical circuit analysis and structural analysis.
-
Finance: Algebraic identities are used in financial calculations, such as compound interest, annuities, and portfolio optimization.
-
Computer Science: Algebraic identities form the basis for algorithms and data structures used in computer science, including cryptography and error detection.
Algebraic identities are not only relevant in Class 9 mathematics but also have widespread applications in various disciplines, making them a crucial topic to master.
Conclusion
In Class 9 mathematics, algebra identities play a vital role in simplifying expressions and solving equations. Understanding basic algebraic identities, expanding and simplifying expressions, factorizing algebraic expressions, and solving equations using algebraic identities are essential skills for students. Moreover, algebraic identities find applications in numerous real-life scenarios and different branches of science and engineering. By grasping the concepts of algebra identities, students lay a strong foundation for higher mathematics and its practical applications.
FAQs
-
What are the most commonly used algebra identities in Class 9?
- The most commonly used algebra identities in Class 9 include the distributive property, associative property, and commutative property.
-
How can I remember and apply algebra identities effectively?
- Practice is key to remembering and applying algebra identities effectively. Regularly solve problems and work on exercises that involve the application of algebraic identities.
-
Can algebra identities be used in other branches of mathematics?
- Yes, algebra identities form the basis for various branches of mathematics, including calculus, linear algebra, and abstract algebra.
-
Are algebra identities relevant beyond Class 9?
- Absolutely! Algebra identities are fundamental concepts that continue to be used in advanced mathematics, as well as in real-world applications in various fields.
-
Are there any online resources to practice algebra identities?
- Yes, there are numerous online resources, such as math practice websites, interactive tutorials, and video lessons, that offer practice problems and explanations for algebra identities. Some popular platforms include Khan Academy, Mathway, and Brilliant.